> x <- 5 > exp(x)# = e5 [1] 148.4132 > exp(2.3)# = e2.3 [1] 9.974182 > exp(-2)# = e-2 [1] 0.1353353
To get the value of the Euler's number (e):
> exp(1)[1] 2.718282
> y <- rep(1:20) > exp(y)
[,1] [,2] [,3] [,4] [,5] [1,] 2.718282 20.08554 148.4132 1096.633 8103.084 [2,] 7.389056 54.59815 403.4288 2980.958 22026.466
^ operator calculates a raised to power b:
> 2^3
[1] 8
> 8 ^ (1/3)[1] 2 > exp(log(8)/3)[1] 2 > exp(log(32)/5)[1] 2
expm1() function computes exp() minus 1:
> expm1(5)# = e5 -1
[1] 147.4132
> expm1(rep(1:20))
[,1] [,2] [,3] [,4] [,5] [1,] 1.718282 19.08554 147.4132 1095.633 8102.084 [2,] 6.389056 53.59815 402.4288 2979.958 22025.466
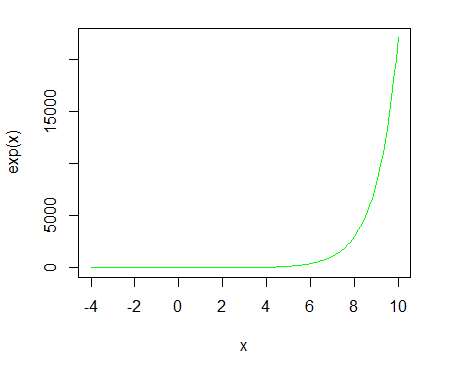
Let's plot the exponential value in the range of -4 ~ 10:
> x <- seq(-4, 10, by=0.1) > plot(x,exp(x),typ="l",col="green")